Podepisujeme se s eliptickými certifikáty, část III: Co jsou zač ty eliptické křivky?
Možnost spoléhat se na elektronické podpisy stojí a padá s výpočetní složitostí matematické úlohy, kterou by zlá protistrana musela vyřešit. Eliptické křivky přinášejí právě takovou úlohu.Tento malý letní seriál (první díl, druhý díl), věnovaný eliptickým křivkám a jejich využití při elektronickém podepisování, by rozhodně nebyl úplný bez alespoň stručné informace o tom, co vlastně jsou eliptické křivky zač a proč se vyplatí používat kryptografii, která je na nich založena.
Tento seriál je ale orientovaný výrazně prakticky, a proto jsem nechtěl čtenáře odradit teorií hned na samém začátku. A nechci to udělat ani teď – protože kolem eliptických křivek a na nich založené kryptografii je opravdu hodně složitá matematika, jejíž popis by patřil do jiného média (a také jinému autorovi).
Naštěstí k praktickému využití výhod, které kryptografie eliptických křivek přináší, není její detailní znalost nutná. Přesto je ale dobré mít alespoň určité tušení, „o co asi jde“. I proto, abychom se nenechali odradit (snad jen dočasnými) problémy, popisovanými v předchozích dvou dílech, a věděli, že přechod na kryptografii eliptických křivek je i v zájmu nás koncových uživatelů.
Dostatečně složitá matematická úloha
O samotné podstatě eliptických křivek bylo již napsáno hodně, a zde se rozhodně nebudu pouštět do dalšího výkladu jejich podstaty. Čtenáře, dychtivé odborného výkladu, si dovolím odkázat například sem či sem. Místo toho si dovolím nabídnout následující zjednodušení:
Abychom se na elektronické podpisy mohli spoléhat a nemuseli se bát, že nám je – v nějaké brzké době, aby to ještě dávalo smysl – protistrana dokáže prolomit (zneužít, napodobit, resp. jakkoli zmanipulovat), musíme pro ně najít takové řešení, aby „řádné“ používání elektronických podpisů bylo jednoduché, ale jejich případné prolomení vyžadovalo vyřešení nějaké výpočetně hodně složité matematické úlohy. Tak složité, aby se to nikomu nevyplatilo ani zkoušet.
Hrajeme zde tedy na to, že protistraně klidně řekneme (resp. nemůžeme před ní utajit), o jakou matematickou úlohu jde a jak by příslušný výpočet při prolamování podpisů musel probíhat. Současně ale musíme mít (my i oni) jistotu, že jiný způsob prolomení není možný a že jediný možný výpočet je skutečně tak složitý, že by dnes dostupným počítačům trval tak dlouho (například nějaké statisíce až miliony let), aby vůbec nemělo smysl s ním začínat.
Jenže: výpočetní síla počítačů neustále raketově roste, a čas potřebný k výpočtu oné hodně složité matematické úlohy se tím také zkracuje. Dokonce mnohem rychleji, než jak plyne čas v kalendáři. Co by dnešním počítačům trvalo nějaké miliony let, mohou ty budoucí – třeba již za několik málo let – zvládnout třeba za den, či jen hodinu.
Dočasně sice můžeme vše trochu kompenzovat parametrizací oné matematické úlohy – konkrétně třeba zvětšováním délky používaných klíčů – ale to nejde dělat libovolně dlouho. Nemusí to stačit a také tím zvyšujeme nároky na výpočetní kapacitu i sami sobě, pro „řádnou“ práci s elektronickými podpisy.
Proto je třeba se poohlížet i po jiných řešeních, která by dosud používanou výpočetně složitou matematickou úlohou nahradilo jinou, ještě složitější úlohou – a díky tomu nám zase po nějakou dobu „vydržela“.
Právě v tomto kontextu je vhodné se dívat na kryptografii eliptických křivek: přináší novou matematickou úlohu s příznivějšími vlastnostmi, než jaké má dosud používaná úloha. Dokáže nabídnout srovnatelnou, či ještě větší míru bezpečnosti (ve smyslu ochrany proti prolomení), a to při nižších nárocích na velikost klíčů a tím i na potřebu výpočetní kapacity pro „řádné“ používání elektronických podpisů (zatímco pro jejich případné prolomení je nezbytný výpočet naopak řádově složitější).
ECC a ECDSA místo RSA
Pro srovnání: dnes dominující řešení elektronických podpisů, založené na algoritmu RSA (které se opírá o matematickou úlohu v podobě faktorizace neboli rozkladu hodně velkých čísel na prvočísla), pracuje s klíči o velikosti 2048 bitů.
Připomeňme si to na následujícím obrázku, který jsme si ukazovali již v prvním dílu tohoto malého seriálu. Jde o kontejnery na soukromé klíče (a k nim vystavené certifikáty) nové eOP: je zde 8 kontejnerů pro klíče generované podle algoritmu RSA, až do velikosti 4096 bitů. Jak ukazuje obrázek, na své eOP mám aktuálně 6 klíčů oné dnes používané velikosti 2048 bitů (viz modře vyplněná políčka).
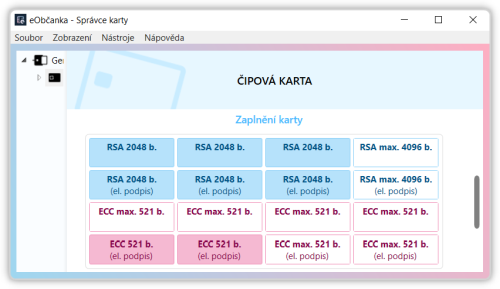
Dále je na nové eOP 8 dalších kontejnerů pro klíče (a certifikáty), generované pomocí algoritmů pracujících s eliptickými křivkami (a onou složitou matematickou úlohou je zde hledání bodů na takovýchto eliptických křivkách, resp. výpočet diskrétních logaritmů). Obecně se přitom hovoří o „kryptografii eliptických křivek“, zkratkou ECC (Elliptic Curve Cryptography), a v případě jejího využití pro elektronické podepisování se hovoří konkrétně o algoritmu ECDSA (Elliptic Curve Digital Signature Algorithm).
Povšimněme si, že „ECC kontejnery“ jsou připraveny pojmout klíče jen do velikosti 521 bitů, a tedy jen o velikosti cca jedné osminy oproti 4096 bitům u RSA. Nezapomínejme ale na to, že „síla“ ECC algoritmů s klíči určité velikosti je podstatně vyšší než u RSA se stejnou velikostí klíčů. A to opravdu podstatně.
Naznačuje to i následující tabulka, uspořádaná podle velikosti oné „síly“ – kterou kryptologové měří podle tzv. „bezpečnostního ekvivalentu v bitech“ (resp. bit security level).
|
„síla“ (bezpečnostní ekvivalent v bitech) |
112 bitů |
128 bitů |
156 bitů |
192 bitů |
256 bitů |
|
RSA s velikostí klíče |
2048 bitů |
3072 bitů |
4096 bitů |
||
|
ECDSA s velikostí klíče |
224 bitů |
256 bitů |
384 bitů |
521 bitů |
Takže třeba dnes běžně používaný algoritmus RSA s klíčem velikosti 2048 bitů je stejně „silný“ jako „eliptický“ algoritmus ECDSA s velikostí klíče 224 bitů. A nejsilnější RSA, co se ještě „vejde“ na novou eOP (s klíči velikosti 4096 bitů), je stále podstatně slabší než ECDSA s velikostí klíče 384. Nehledě pak na ECDSA s 521bitovými klíči.
Další výhody kryptografie eliptických křivek
Nastiňme si alespoň stručně další výhody „eliptických“ řešení: kromě větší „síly“ (měřené v bezpečnostním ekvivalentu v bitech) a menších klíčů to jsou menší nároky na výpočetní kapacitu pro „řádné“ používání, ale i na přenosovou kapacitu (např. samotné podpisy jsou také menší). Proto jsou řešení, založená na kryptografii eliptických křivek, vhodná jak pro podepisování elektronických dokumentů (v analogii k vlastnoručnímu podepisování listinných dokumentů), tak i pro celou širokou škálu účelů, které nějakým způsobem využívají technologie elektronických podpisů v prostředí, kde je třeba šetřit s výpočetní i přenosovou kapacitou. Nebo kde jen není úplně vhodné s ní plýtvat.
Proto je kryptografie eliptických křivek velmi atraktivní například pro nejrůznější mobilní řešení. Dále tam, kde se elektronickým podepisováním zajišťuje integrita (neporušenost) velkého množství záznamů o nejrůznějších transakcích a každý byte režie navíc hraje svou roli.
„Eliptické“ SSL certifikáty jsou výhodné i pro potřeby autentizace serverů a zabezpečení spojení klientů s nimi, v rámci SSL/TLS, kde také každý byte režie hraje svou roli. Problematikou jejich praktického používání se nedávno zabýval tento článek.
Podepisování není jen o RSA či ECDSA
K dokreslení celé problematiky si ještě musíme říci, že kryptografické algoritmy, jako je RSA a ECDSA, jsou jen částí toho, na čem jsou založeny a co ke svému fungování potřebují elektronické podpisy. Tedy alespoň ty „kryptografické“, založené na kryptografických metodách a algoritmech. Naše (a unijní) právní úprava je označuje jako zaručené elektronické podpisy (anglicky: Advanced Electronic Signatures, zkratkou AdES), zatímco v zámoří se o nich mluví jako o digitálních podpisech. Vynecháváme tedy tzv. prosté elektronické podpisy, které nemusí mít vůbec žádné vlastnosti, funkce ani přínosy, a nejsou na ně kladeny ani žádné požadavky (jde například o něčí jméno, napsané v dokumentu, či o nějakou ikonu, obrázek apod.).
U „kryptografických“ (digitálních, zaručených, resp. AdES) podpisů bychom měli mluvit o celých podpisových schématech, které zahrnují i další důležité „složky“. Algoritmy jako RSA či ECDSA jsou tzv. podpisové algoritmy a slouží k tomu, aby se pomocí soukromého klíče zašifrovala podepisovaná data – čímž vznikne výsledný elektronický podpis.
Nicméně: aby se podle podpisového algoritmu dalo něco zašifrovat, musí být nejprve vygenerován soukromý klíč (i jemu odpovídající veřejný klíč). Součástí podpisového schématu proto je i způsob generování soukromého klíče. Ten je vždy předurčen konkrétním podpisovým algoritmem (neboť ten vždy vyžaduje určitý konkrétní způsob generování soukromého klíče).
Dále: podpisové algoritmy ke svému fungování (zašifrování určitých dat) potřebují, aby tato data měla určitou konkrétní velikost. Jako uživatelé ale potřebujeme podepisovat libovolně velké dokumenty – proto nejprve dochází ke „zmenšení“ podepisovaných dat, cestou vytvoření jejich tzv. otisku (tzv. hash-e). K tomu je nutné použít vhodnou hashovací funkci (hash function).
Hashovacích funkcí existuje vícero a s postupem času také ztrácejí na své „síle“ a bezpečnosti – a proto je třeba včas přecházet na „silnější“. Například od roku 2010 by se již neměla používat hashovací funkce SHA-1, natož pak ještě starší a slabší MD5. Dnes se používá celá skupina hashovacích funkcí, známá jako SHA2, kterou tvoří funkce SHA-224, SHA-256, SHA-384 a SHA-512. Časem, až nám kryptologové řeknou, budeme muset přejít na novější skupinu hashovacích funkcí SHA-3.
Ještě další důležitou součástí podpisových schémat může být tzv. padding: je nutný v případě, kdy je výstup hashovací funkce (otisk, resp. tzv. hash) jinak velkým blokem dat, než jaký vyžaduje podpisový algoritmus – a tak je nutné jej vhodně „vycpat“ (doplnit dalšími daty) na potřebnou velikost.
S potřebou doplnit vhodnou „vycpávku“ (padding) se setkáváme hlavně u podpisového algoritmu RSA, a pro konkrétní volbu přidávaných dat (padding-u) existuje více možností. Programy Adobe Acrobat a Acrobat Reader DC dnes používají padding dle standardu PKCS#1 v1.5, jehož bezpečnost je dnes již problematická (viz např. zde či zde). Přesto tato varianta u elektronických podpisů v běžné praxi (i u podpisů vytvářených jinými nástroji) zcela dominuje.
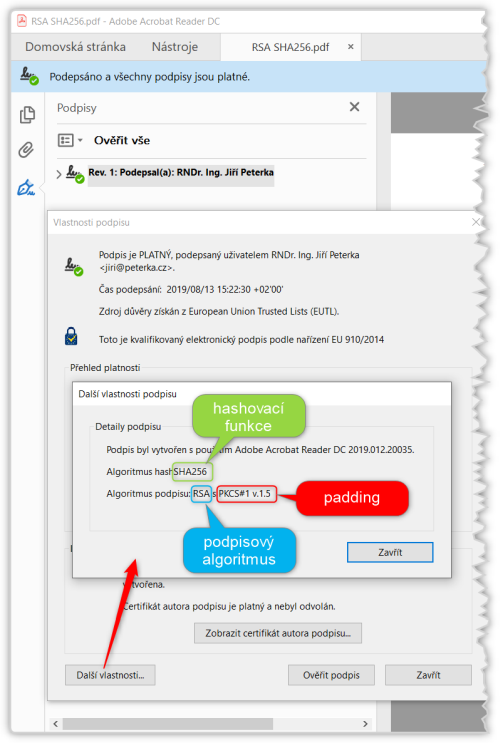
Jaká podpisová schémata mohou podepisující osoby volit?
O tom, se kterými podpisovými schématy (hlavně: kombinacemi podpisového algoritmu a hashovací funkce, případně paddingu) mohou uživatelé v praxi pracovat, rozhodují schopnosti jimi používaných nástrojů – jak aplikací, tak i úložišť soukromých klíčů, tedy např. čipových karet a tokenů, včetně jejich ovladačů – ale stejně tak i výčet certifikátů, které má konkrétní uživatel právě k dispozici.
Závislost na certifikátu je dána už tím, že párová data – soukromý a veřejný klíč – jsou vždy generována podle požadavků a pravidel konkrétního podpisového algoritmu, a v případě algoritmu ECDSA i podle konkrétní eliptické křivky. Ostatně, podle použité křivky mají „eliptické“ soukromé klíče i konkrétní velikost v bitech.
V certifikátu je pak vždy uvedeno, jak velký je (kolik bitů má) veřejný klíč, a tím i soukromý klíč. A také pro který podpisový algoritmus byl veřejný klíč (spolu se soukromým klíčem) vygenerován. Ostatně, proto se také mluví o „eliptických“ certifikátech (resp. ECC či ECDSA certifikátech), pro odlišení od „RSA certifikátů“.
Příklady „eliptických“ certifikátů, po řadě s křivkami P-256, P-384 a P-521, ukazuje následující obrázek, doplněný (zprava) pro srovnání jedním „RSA certifikátem“.
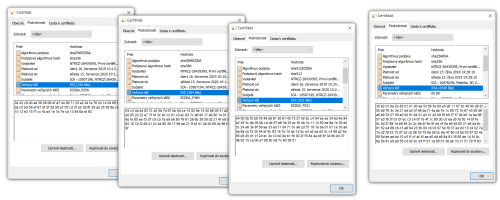
Jinými slovy: pokud chci při podepisování ovlivnit podpisový algoritmus a velikost klíče, musím zvolit (a samozřejmě mít k dispozici) odpovídající podpisový certifikát.
Pokud jde o hashovací funkci, která má být použita při vytváření podpisu, možnost jejího výběru už záleží na možnostech a nastavení těch aplikací, karet, tokenů a ovladačů, které podepisující osoba využívá.
Například Adobe Acrobat Reader DC podporuje hashovací funkce MD5, RIPEMD160, SHA1, SHA256, SHA384 a SHA512. Od verze 9.1 sám standardně použije SHA256, ale pokud uživatel ví, jak (přes registry), může si předepsat použití jiné hashovací funkce. Příklady ukazuje následující obrázek – jde o podpisy založené na stejném („RSA“) certifikátu, ale s použitím různých hashovacích funkcí.
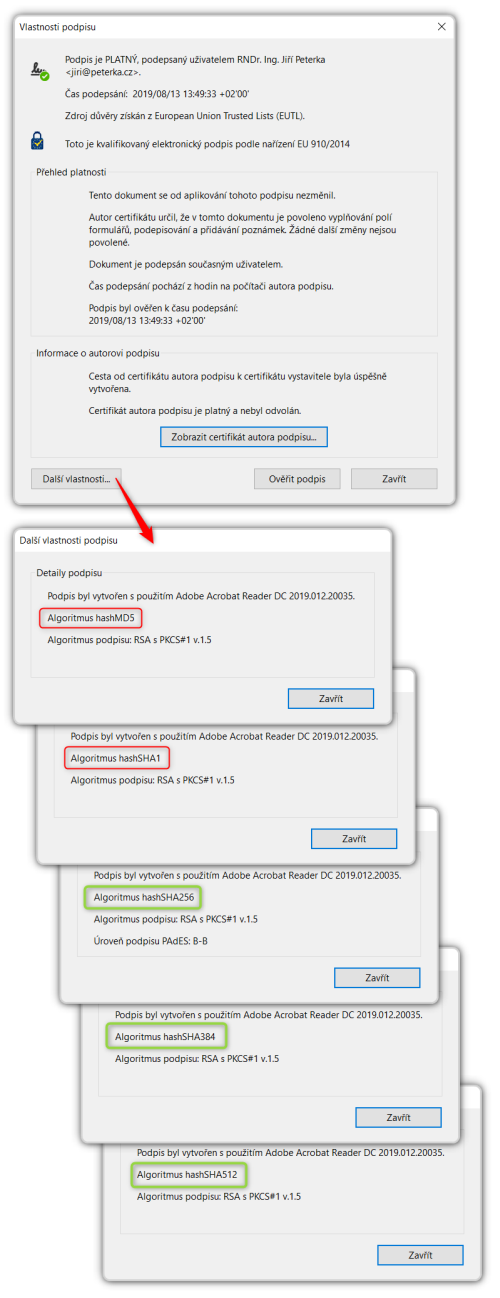
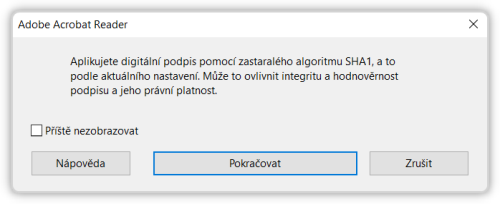
Znovu si ale zdůrazněme, že ne každá hashovací funkce je dostatečně silná. Na to, že třeba už i SHA1 je dnes již zastaralá (a neměla by se používat již od roku 2010), uživatele upozorní i sám Adobe Acrobat Reader.
Právě popsaná možnost volit si hashovací funkci ale u Adobe Acrobat Readeru platí jen v souvislosti s podpisovým algoritmem RSA. Pro ECDSA a „eliptické“ certifikáty si Reader volí hashovací funkci sám, podle křivky (resp. podle jí odpovídající velikosti soukromého klíče), a není možné mu předepsat použití jiné hashovací funkce. Hashovací funkci Reader volí podle této tabulky (zdroj):
|
křivka, podporovaná v rámci ECDSA |
hashovací funkce |
|
P-256 (secp256r1) |
SHA-256 |
|
P-384 (secp384r1) |
SHA-384 |
|
P-521 (secp521r1) |
SHA-512 |
Takže když jsem v Adobe Acrobat Readeru pomocí svého nového „eliptického“ certifikátu (s křivkou P-521, resp. secpr521r1) vytvořil kvalifikovaný elektronický podpis, Reader automaticky použil hashovací funkci SHA512. A pochopitelně podpisový algoritmu ECDSA, jak ostatně ukazuje i následující obrázek.
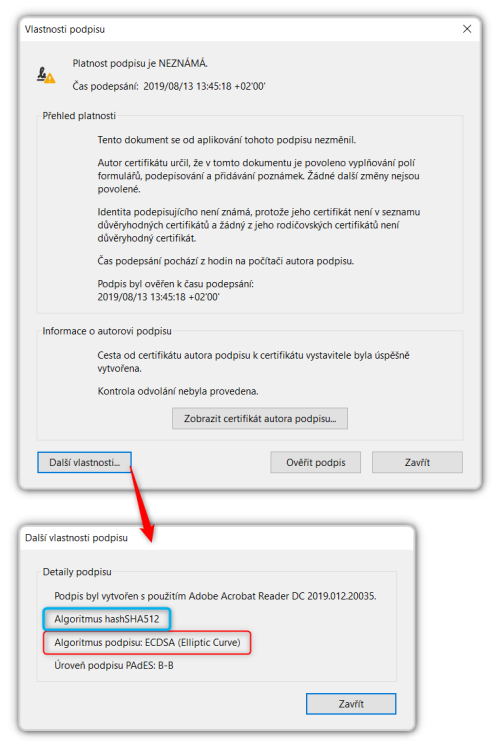
Nicméně když jsem použil jinou aplikaci (konkrétně „unijní“ podepisovací Java applet), již jsem si mohl zvolit i hashovací funkci, kterou chci použít pro podpis, založený na mém „eliptickém“ certifikátu – s pevnou délkou klíče 521 bitů. Různé varianty takovýchto podpisů, ověřované opět v Adobe Acrobat Readeru, ukazuje následující obrázek.
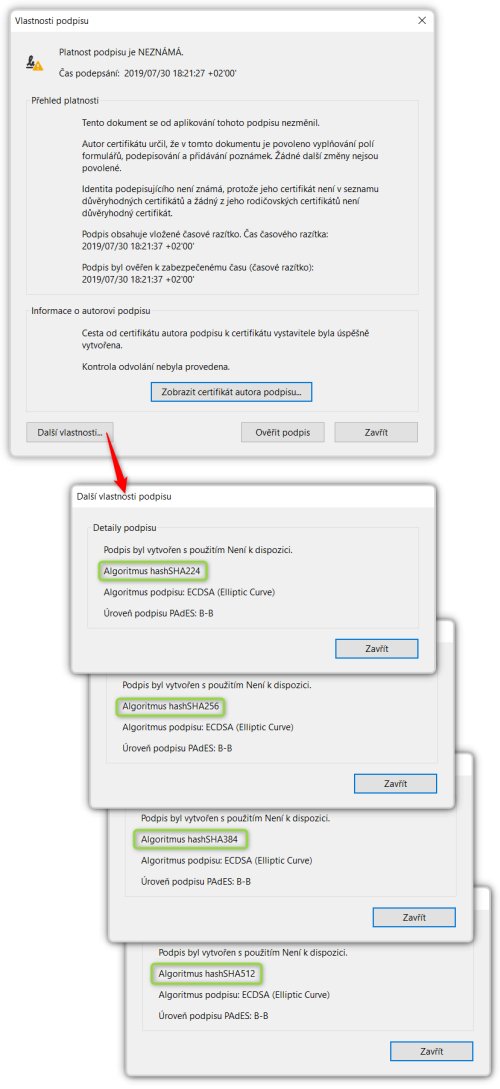
Eliptické křivky jsou budoucností, ale...
Kryptografie eliptických křivek je určitě budoucností, která nás – nejenom v oblasti elektronických podpisů – určitě čeká a nemine. Jak jsme si ukázali v první dílu tohoto malého seriálu, pokud jde o vytváření „eliptických“ podpisů, je situace relativně dobrá a řada nástrojů s touto novou technologií dokáže pracovat.
Horší je to na straně těch, kteří elektronicky podepsané dokumenty přijímají a mají se spoléhat na jejich autenticitu a právní validitu (odvozovanou z platnosti elektronických podpisů a pečetí těchto dokumentů). Pravdou je, že situace se zde může lepšit doslova den ze dne – jak dokazuje i to, že v době mezi vydáním prvního a druhého dílu se s „eliptickými“ certifikáty od I.CA naučily pracovat programy Adobe Acrobat a Acrobat Reader DC. Již od začátku (od umístění na unijní seznam LOTL) přitom s „eliptickými“ podpisy umí pracovat kvalifikované služby pro ověřování (SecuSign a QVerify).
Jinde, hlavně asi ve veřejné správě, to ale nejspíše bude trvat déle. Připomeňme si, v souvislosti s prvním dílem, že s elektronickými podpisy, založenými na „eliptických“ certifikátech, si dosud neporadí například Daňový portál. Stejně tak si s nimi ještě neporadí třeba podatelny soudů. A bohužel ani CzechPOINTy – takže na autorizované konverze z „elipticky“ podepsaných elektronických dokumentů do listinné podobě prozatím zapomeňte.
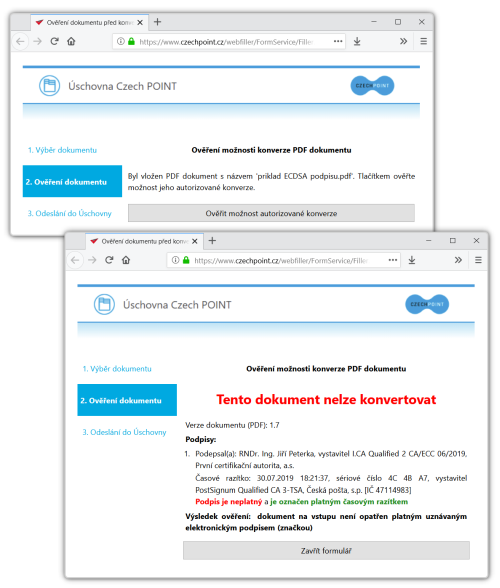
Na závěr tohoto článku i celého třídílného seriálu si dovolím připomenout, že testovací dokument s kvalifikovaným „eliptickým“ podpisem najdete zde – a tak si můžete sami vyzkoušet, jak si s ním poradí vámi používaný nástroj pro ověřování platnosti. Například vaše spisová službu. Za případný feedback předem děkuji.